风格转移

这几天看了一篇风格转移的论文，这里大致介绍下论文的内容，并且推到下论文中出现的公式。

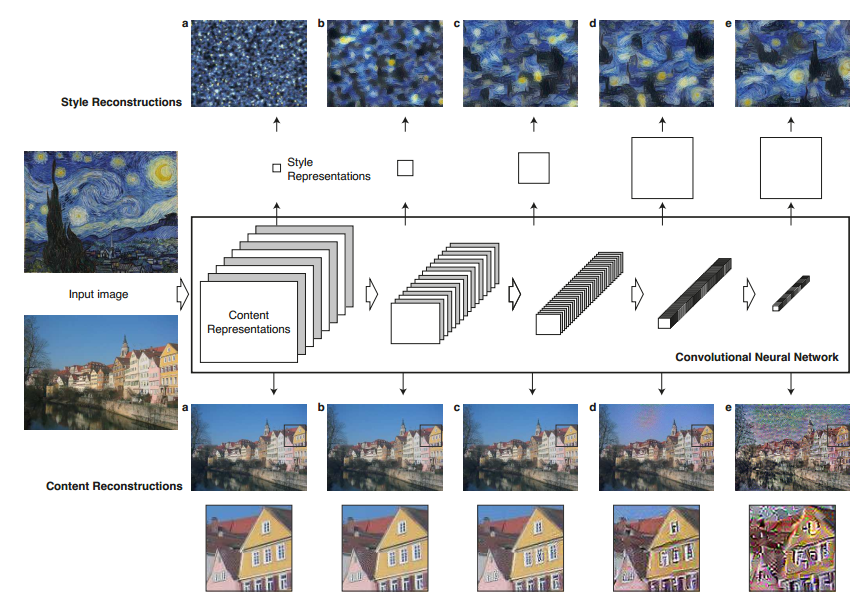
基本思想

有两张图片，我们关注一张图片的内容(Content)记为C，一张图片的风格(Style)记为S，想要生成一张图片包含C的内容和S的风格，记为G。

那么如何获取图片的C和S那？论文使用训练好的VGG net解决这一问题。

文中使用VGG net的中间层来表示C：对于一张input_image，中间某一输出层shape为$height\times width \times channel$，将其reshape成$(channel \times (height * width))$。这样便得到了C，简单的理解是使用训练好的VGG net对图片进行再编码。为公式推导方便我们记为$F_{N \times M}$，N为特征图的数量，M为特征图的大小。

对于S的表示略微复杂：在VGG net的某一层，得到了该层的feature maps，计算这些feature maps的特征相关性feature correlations，就可以得到这一层的“风格表示”，最终的S是多个层的“风格表示”的线性组合。

怎么计算feature correlations那？文中介绍了使用Gram Matrix的方法。

[G_{ij}^{l}=\sum_{k}F_{ik}^{l}F_{jk}^{l}]

从定义可以看出，Gram阵是对称阵，我们公式推导会多次用到这一性质。

loss定义

论文中定义的Loss是对ContentLoss和StyleLoss进行加权求和。

[\mathcal{L}{total}=\alpha\mathcal{L}{content}+\beta\mathcal{L}_{style}]

其中$\alpha$和$\beta$是超参数

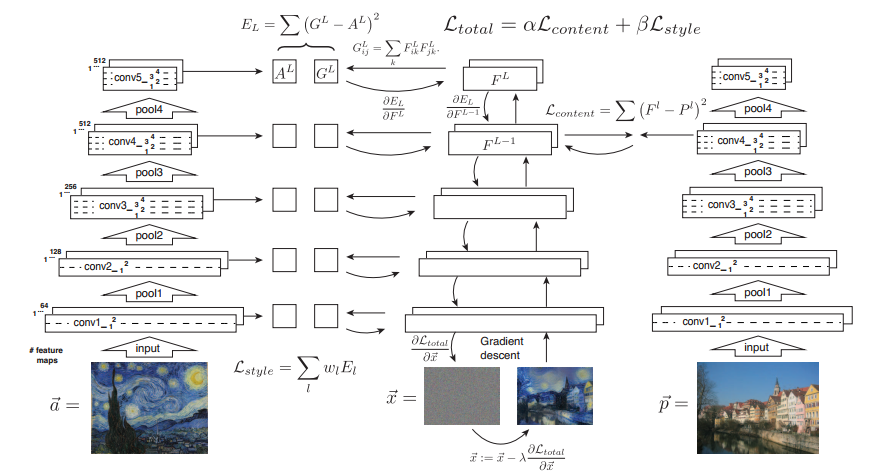
ContentLoss

为公式推到方便，先来定义几个符号

$\overrightarrow{p}$: 原始图像

$\overrightarrow{x}$: 生成图像

$l$: VGG net的第$l$层

$F^l$: 原始图像在VGG net第$l$层的内容特征表示

$P^l$: 生成图像在VGG net第$l$层的内容特征表示

ContentLoss定义为

[\mathcal{L}{content}(\overrightarrow{p}, \overrightarrow{x}, l)=\frac{1}{2}\sum{i,j}(F^l_{ij}-P^l_{ij})^2]

误差对$l$层每一激活值的偏导

[\frac{\partial{\mathcal{L}{content}}}{\partial{F^l{ij}}}=\left{ \begin{aligned} &(F^l-P^l){ij} \qquad &if \ F^l{ij}>0
&0 &if \ F^l_{ij}<0 \end{aligned} \right.]

这一步偏导好求，就是当$F^l_{ij}<0$时偏导是0，文中没有做解释

StyleLoss

$\overrightarrow{a}$: 原始图像

$\overrightarrow{x}$: 生成图像

$l$: VGG net的第$l$层

$A^l$: 原始图像在VGG net第$l$层的风格特征表示

$G^l$: 生成图像在VGG net第$l$层的风格特征表示

第$l$层的StyleLoss定义为

[E_l=\frac{1}{4N_l^2M^2l}\sum{i,j}{(G^l_{ij}-A^l_{ij})^2}]

TotalStyleLoss定义为

[\mathcal{L}{style}(\overrightarrow{a},\overrightarrow{x})=\sum{l=0}^{L}w_lE_l]

误差对$l$层每一激活值的偏导

[\frac{\partial{E_l}}{\partial{F^l_{ij}}}=\left{ \begin{aligned} &\frac{1}{N^2l M^2_l}((F^l)^T(G^l-A^l)){ji} &if \ F^l_{ij}>0
&0 &if \ F^l_{ij}<0 \end{aligned} \right.]

接下来是推导过程

[\frac{\partial{E_l}}{\partial{F^l_{ij}}}=\frac{\partial{E_l}}{\partial{G^l}} \frac{\partial{G^l}}{\partial{F^l_{ij}}}=\sum_{m,n}^N\frac{\partial{E_l}}{\partial{G^l_{mn}}} \frac{\partial{G^l_{mn}}}{\partial{F^l_{ij}}}]

考虑这个式子$\frac{\partial{G^l_{mn}}}{\partial{F^l_{ij}}}$

当$m\neq i,n\neq i$时，上式为0

当$m=i,n\neq i$时，上式为$F_{nj}$

当$m\neq i,n=i$时，上式为$F_{mj}$

当$m=i,n=i$时，上式为$F_{ij}$

[\therefore \sum_{m,n}^N\frac{\partial{E_l}}{\partial{G^l_{mn}}} \frac{\partial{G^l_{mn}}}{\partial{F^l_{ij}}}= \sum_{n,n\neq i}^N{\frac{\partial{E_l}}{\partial{G^l_{in}}}F_{nj}} + \sum_{m,m\neq i}^N{\frac{\partial{E_l}}{\partial{G^l_{mi}}}F_{mj}} + 2\frac{\partial{E_l}}{\partial{G^l_{ii}}}F_{ij}]

又

[\because \sum_{n,n\neq i}^N{\frac{\partial{E_l}}{\partial{G^l_{in}}}F_{nj}} + \frac{\partial{E_l}}{\partial{G^l_{ii}}}F_{ij} = 2[(G_{i1}-A_{i1})F_{1j} + (G_{i2}-A_{i2})F_{2j} + \cdots+ (G_{iN}-A_{iN})F_{Nj}]]

[\because \sum_{m,m\neq i}^N{\frac{\partial{E_l}}{\partial{G^l_{mi}}}F_{mj}} + \frac{\partial{E_l}}{\partial{G^l_{ii}}}F_{ij} = 2[(G_{1i}-A_{1i})F_{1j} + (G_{2i}-A_{2i})F_{2j} + \cdots+ (G_{Ni}-A_{Ni})F_{Nj}]]

利用Gram矩阵的对称性得

[\sum_{n,n\neq i}^N{\frac{\partial{E_l}}{\partial{G^l_{in}}}F_{nj}}+ \frac{\partial{E_l}}{\partial{G^l_{ii}}}F_{ij}=\sum_{m,m\neq i}^N{\frac{\partial{E_l}}{\partial{G^l_{mi}}}F_{mj}}+ \frac{\partial{E_l}}{\partial{G^l_{ii}}}F_{ij}]

[\therefore \frac{\partial{E_l}}{\partial{F^l_{ij}}}=\frac{1}{N^2lM^2_l} \sum_k^N{(G^l-A^l){ik}F^l_{kj}}=\frac{1}{N^2lM^2_l}((G^l-A^l)F^l){ij}=\frac{1}{N^2lM^2_l} ((F^l)^T(G^l-A^l)){ji}]

论文实现

link

Content	Style	Generate

Acknowledgement

Image Style Transfer Using Convolutional Neural Networks by Gatys et al. CVPR 2016

Neural Transfer with PyTorch