前段时间学习了 mlc.ai 提供的机器学习编译的相关课程，本文简单做个总结，回顾下机器学习编译的基本思想。

机器学习编译基本思想

什么是机器学习编译

mlc.ai 中对机器学习编译的定义如下：

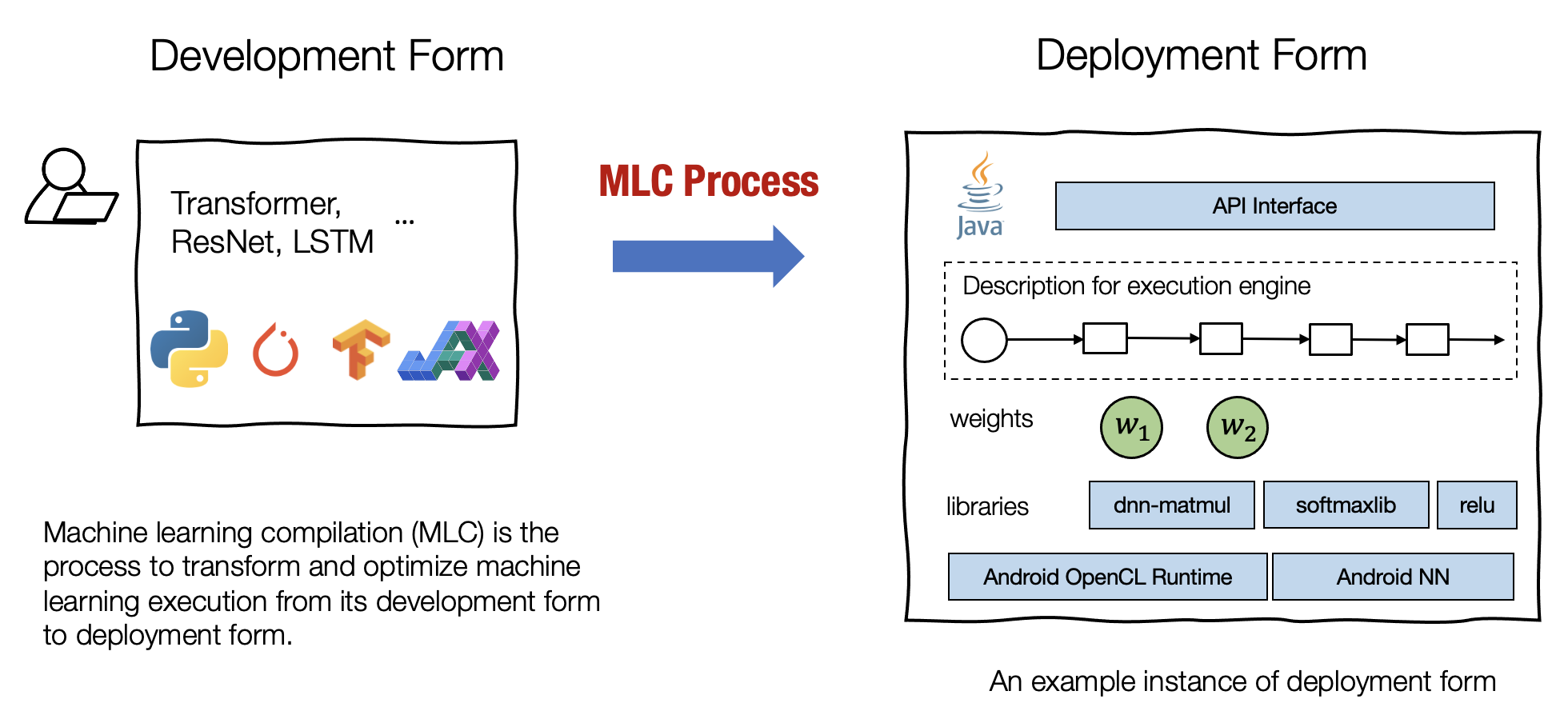
机器学习编译 (machine learning compilation, MLC) 是指，将机器学习算法从开发阶段，通过变换和优化算法，使其变成部署状态。

开发形式是指我们在开发机器学习模型时使用的形式。典型的开发形式包括用 Paddle、PyTorch、TensorFlow 或 JAX 等通用框架编写的模型描述，以及与之相关的权重。

部署形式是指执行机器学习应用程序所需的形式。它通常涉及机器学习模型的每个步骤的支撑代码、管理资源（例如内存）的控制器，以及与应用程序开发环境的接口（例如用于 android 应用程序的 java API）。（摘抄自 mlc 课件）

definition

机器学习编译的目的：

集成与最小化依赖 部署过程通常涉及集成 (Integration)，即将必要的元素组合在一起以用于部署应用程序。例如，如果我们想启用一个安卓相机应用程序来检测猫，我们将需要图像分类模型的必要代码，但不需要模型无关的其他部分（例如，我们不需要包括用于 NLP 应用程序的embedding table）。代码集成、最小化依赖项的能力能够减小应用的大小，并且可以使应用程序部署到的更多的环境。

利用硬件加速 每个部署环境都有自己的一套原生加速技术，并且其中许多是专门为机器学习开发的。机器学习编译的一个目标就是是利用硬件本身的特性进行加速。我们可以通过构建调用原生加速库的部署代码或生成利用原生指令（如 TensorCore）的代码来做到这一点。

通用优化 有许多等效的方法可以运行相同的模型执行。 MLC 的通用优化形式是不同形式的优化，以最小化内存使用或提高执行效率的方式转换模型执行。 (摘抄自 mlc 课件)

TVM中的一些概念及编译的思路

workflow

上图是 tvm 的编译流程，外部的模型（paddle、pytorch等）导入得到 relay/relax 的高层 ir 表示，进一步 lower 后得到底层 tensor ir 表示，进一步编译可得到可执行的机器码；

IRModule 和 runtime::Module

IRModule 是程序变换的核心组件，其内部hold了一系列 Function（可以是relay/relax::Function 也可以是 tir::PrimFunc）；

class IRModuleNode : public Object {
 public:
  /*! \brief A map from ids to all global functions. */
  Map<GlobalVar, BaseFunc> functions;
  ...

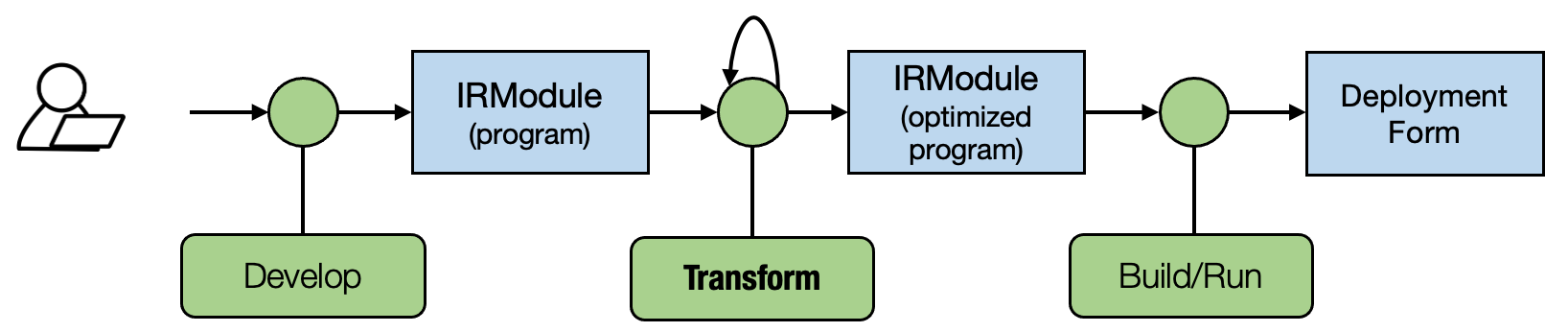
机器学习编译的基本思想就是变换：对于相同的计算逻辑进行等价的变换，使其访存更加友好、尽可能的适配底层硬件的特殊指令集等； mlc_process

runtime::Module 是 IRModule 的编译产物，可接受输入、运行、返回输出，类似于执行器；(目前不是我们关注的重点)

ir_module = ...
with tvm.transform.PassContext(opt_level=3):
    rt_mod = tvm.build(ir_module, target)
output = rt_mod['main'](input, ...)

TensorIR 与 Schedule 变换

TensorIR 是 TVM 中针对 tensor 的计算过程的描述（DSL）

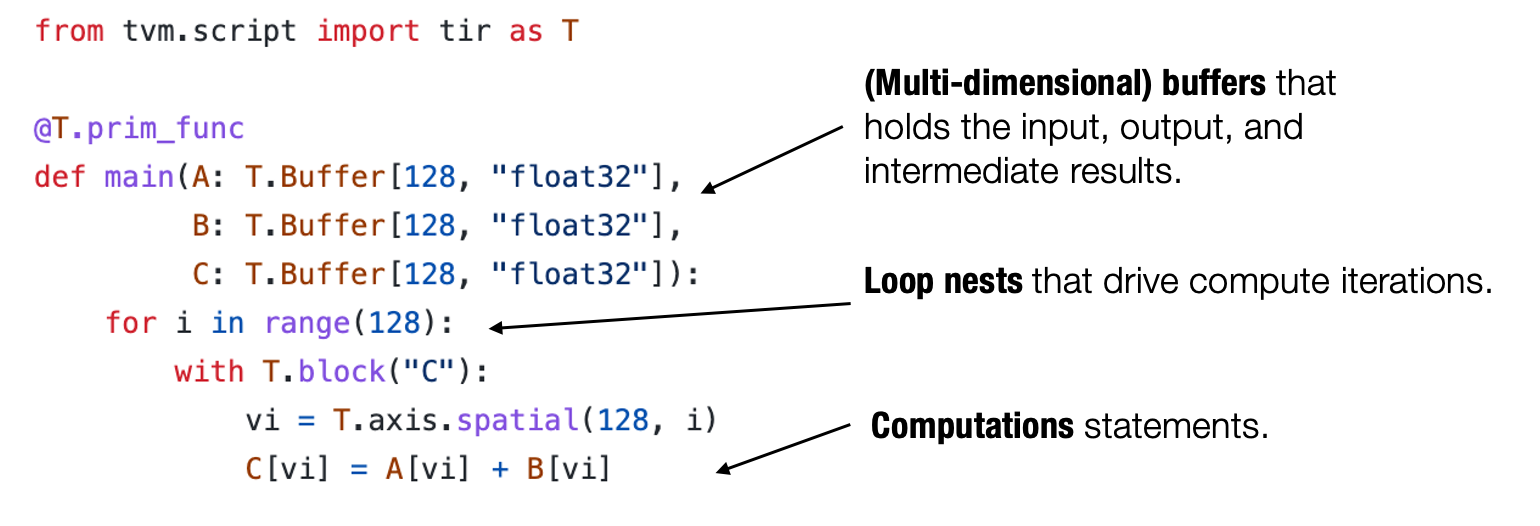
tensor_ir

再看一个 matmul + relu 的 TensorIR 表示和 numpy 的对比（可以一一对应）

tensor_func_and_numpy

Schedule 程序变换的基本组件，tvm 提供了多种方法，可参考官方文档

举例，针对上述的 matmul + relu 进行变换

原始的 IRModule 如下：

@tvm.script.ir_module
class Module:
    @T.prim_func
    def mm_relu(A: T.Buffer[(128, 128), "float32"], B: T.Buffer[(128, 128), "float32"], C: T.Buffer[(128, 128), "float32"]) -> None:
        # function attr dict
        T.func_attr({"global_symbol": "mm_relu", "tir.noalias": True})
        # body
        # with T.block("root")
        Y = T.alloc_buffer([128, 128], dtype="float32")
        for i, j, k in T.grid(128, 128, 128):
            with T.block("Y"):
                vi, vj, vk = T.axis.remap("SSR", [i, j, k])
                T.reads(A[vi, vk], B[vk, vj])
                T.writes(Y[vi, vj])
                with T.init():
                    Y[vi, vj] = T.float32(0)
                Y[vi, vj] = Y[vi, vj] + A[vi, vk] * B[vk, vj]
        for i, j in T.grid(128, 128):
            with T.block("C"):
                vi, vj = T.axis.remap("SS", [i, j])
                T.reads(Y[vi, vj])
                T.writes(C[vi, vj])
                C[vi, vj] = T.max(Y[vi, vj], T.float32(0))

进行 split 变换

sch = tvm.tir.Schedule(MyModule)
block_Y = sch.get_block("Y", func_name="mm_relu")
i, j, k = sch.get_loops(block_Y)
j0, j1 = sch.split(j, factors=[None, 4])

变换后的 IRModule 如下：

@tvm.script.ir_module
class Module:
    @T.prim_func
    def mm_relu(A: T.Buffer[(128, 128), "float32"], B: T.Buffer[(128, 128), "float32"], C: T.Buffer[(128, 128), "float32"]) -> None:
        # function attr dict
        T.func_attr({"global_symbol": "mm_relu", "tir.noalias": True})
        # body
        # with T.block("root")
        Y = T.alloc_buffer([128, 128], dtype="float32")
        for i, j_0, j_1, k in T.grid(128, 32, 4, 128):
            with T.block("Y"):
                vi = T.axis.spatial(128, i)
                vj = T.axis.spatial(128, j_0 * 4 + j_1)
                vk = T.axis.reduce(128, k)
                T.reads(A[vi, vk], B[vk, vj])
                T.writes(Y[vi, vj])
                with T.init():
                    Y[vi, vj] = T.float32(0)
                Y[vi, vj] = Y[vi, vj] + A[vi, vk] * B[vk, vj]
        for i, j in T.grid(128, 128):
            with T.block("C"):
                vi, vj = T.axis.remap("SS", [i, j])
                T.reads(Y[vi, vj])
                T.writes(C[vi, vj])
                C[vi, vj] = T.max(Y[vi, vj], T.float32(0))

reorder 变换：

sch.reorder(j0, k, j1)

@tvm.script.ir_module
class Module:
    @T.prim_func
    def mm_relu(A: T.Buffer[(128, 128), "float32"], B: T.Buffer[(128, 128), "float32"], C: T.Buffer[(128, 128), "float32"]) -> None:
        # function attr dict
        T.func_attr({"global_symbol": "mm_relu", "tir.noalias": True})
        # body
        # with T.block("root")
        Y = T.alloc_buffer([128, 128], dtype="float32")
        for i, j_0, k, j_1 in T.grid(128, 32, 128, 4):
            with T.block("Y"):
                vi = T.axis.spatial(128, i)
                vj = T.axis.spatial(128, j_0 * 4 + j_1)
                vk = T.axis.reduce(128, k)
                T.reads(A[vi, vk], B[vk, vj])
                T.writes(Y[vi, vj])
                with T.init():
                    Y[vi, vj] = T.float32(0)
                Y[vi, vj] = Y[vi, vj] + A[vi, vk] * B[vk, vj]
        for i, j in T.grid(128, 128):
            with T.block("C"):
                vi, vj = T.axis.remap("SS", [i, j])
                T.reads(Y[vi, vj])
                T.writes(C[vi, vj])
                C[vi, vj] = T.max(Y[vi, vj], T.float32(0))

reverse_compute_at 变换：

block_C = sch.get_block("C", "mm_relu")
sch.reverse_compute_at(block_C, j0)

@tvm.script.ir_module
class Module:
    @T.prim_func
    def mm_relu(A: T.Buffer[(128, 128), "float32"], B: T.Buffer[(128, 128), "float32"], C: T.Buffer[(128, 128), "float32"]) -> None:
        # function attr dict
        T.func_attr({"global_symbol": "mm_relu", "tir.noalias": True})
        # body
        # with T.block("root")
        Y = T.alloc_buffer([128, 128], dtype="float32")
        for i, j_0 in T.grid(128, 32):
            for k, j_1 in T.grid(128, 4):
                with T.block("Y"):
                    vi = T.axis.spatial(128, i)
                    vj = T.axis.spatial(128, j_0 * 4 + j_1)
                    vk = T.axis.reduce(128, k)
                    T.reads(A[vi, vk], B[vk, vj])
                    T.writes(Y[vi, vj])
                    with T.init():
                        Y[vi, vj] = T.float32(0)
                    Y[vi, vj] = Y[vi, vj] + A[vi, vk] * B[vk, vj]
            for ax0 in T.serial(4):
                with T.block("C"):
                    vi = T.axis.spatial(128, i)
                    vj = T.axis.spatial(128, j_0 * 4 + ax0)
                    T.reads(Y[vi, vj])
                    T.writes(C[vi, vj])
                    C[vi, vj] = T.max(Y[vi, vj], T.float32(0))

以上都是对 IRModule 的变换，对相同计算的不同描述；现有计算机体系结构的原因，通过程序变换，使其访存更加友好，整体性能也会更好。

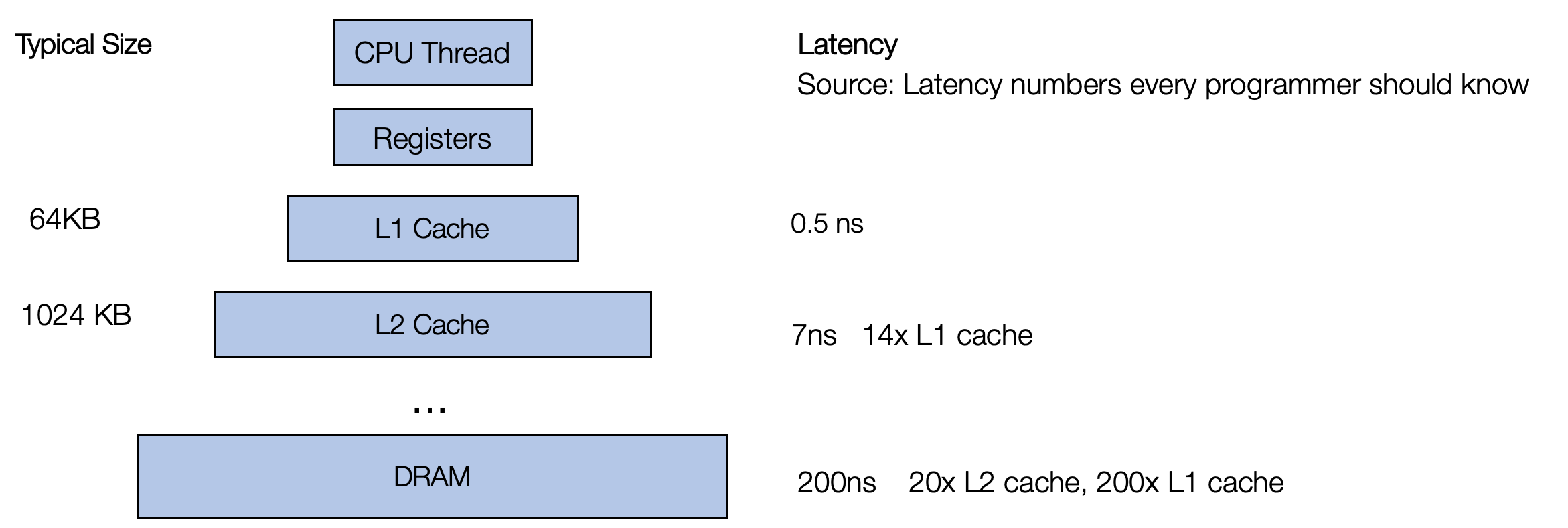
要了解为什么不同的循环变体会导致不同的性能，我们需要回顾一个事实，即访问 A 和 B 中的任何内存块的速度并不一致。现代 CPU 带有多级缓存，需要先将数据提取到缓存中，然后 CPU 才能访问它。

重要的是，访问已经在缓存中的数据要快得多。CPU 采用的一种策略是获取彼此更接近的数据。当我们读取内存中的一个元素时，它会尝试将附近的元素（更正式的名称为“缓存行”）获取到缓存中。因此，当你读取下一个元素时，它已经在缓存中。因此，具有连续内存访问的代码通常比随机访问内存不同部分的代码更快。（摘抄自mlc课件）

上述是人工进行 schedule 变换的例子，也可以通过自动程序优化的方式（搜索空间 + 搜索方法）进行性能优化，TVM 中称为 Meta-Schedule；针对128x128x128的矩阵乘，启用自动程序优化，看下搜索得到的一条优化路径。（相比初始版本性能优化很多，一定程度上能和专家优化的工业级库进行对比）。

b0 = sch.get_block(name="C", func_name="main")
b1 = sch.get_block(name="root", func_name="main")
sch.annotate(block_or_loop=b0, ann_key="meta_schedule.tiling_structure", ann_val="SSRSRS")
l2, l3, l4 = sch.get_loops(block=b0)
v5, v6, v7, v8 = sch.sample_perfect_tile(loop=l2, n=4, max_innermost_factor=64, decision=[4, 1, 32, 1])
l9, l10, l11, l12 = sch.split(loop=l2, factors=[v5, v6, v7, v8], preserve_unit_iters=True)
v13, v14, v15, v16 = sch.sample_perfect_tile(loop=l3, n=4, max_innermost_factor=64, decision=[4, 1, 8, 4])
l17, l18, l19, l20 = sch.split(loop=l3, factors=[v13, v14, v15, v16], preserve_unit_iters=True)
v21, v22 = sch.sample_perfect_tile(loop=l4, n=2, max_innermost_factor=64, decision=[64, 2])
l23, l24 = sch.split(loop=l4, factors=[v21, v22], preserve_unit_iters=True)
sch.reorder(l9, l17, l10, l18, l23, l11, l19, l24, l12, l20)
b25 = sch.cache_write(block=b0, write_buffer_index=0, storage_scope="global")
sch.reverse_compute_at(block=b25, loop=l18, preserve_unit_loops=True)
sch.annotate(block_or_loop=b1, ann_key="meta_schedule.parallel", ann_val=16)
sch.annotate(block_or_loop=b1, ann_key="meta_schedule.vectorize", ann_val=64)
v26 = sch.sample_categorical(candidates=[0, 16, 64, 512], probs=[0.25, 0.25, 0.25, 0.25], decision=1)
sch.annotate(block_or_loop=b1, ann_key="meta_schedule.unroll_explicit", ann_val=v26)
sch.enter_postproc()
b27 = sch.get_block(name="root", func_name="main")
sch.unannotate(block_or_loop=b27, ann_key="meta_schedule.parallel")
sch.unannotate(block_or_loop=b27, ann_key="meta_schedule.vectorize")
sch.unannotate(block_or_loop=b27, ann_key="meta_schedule.unroll_explicit")
b28, b29 = sch.get_child_blocks(b27)
l30, l31, l32, l33, l34, l35, l36, l37, l38, l39 = sch.get_loops(block=b28)
l40 = sch.fuse(l30, l31, l32, l33, preserve_unit_iters=True)
sch.parallel(loop=l40)
l41 = sch.fuse(l39, preserve_unit_iters=True)
sch.vectorize(loop=l41)
sch.annotate(block_or_loop=l40, ann_key="pragma_auto_unroll_max_step", ann_val=16)
sch.annotate(block_or_loop=l40, ann_key="pragma_unroll_explicit", ann_val=1)
l42, l43, l44 = sch.get_loops(block=b29)
l45 = sch.fuse(l44, preserve_unit_iters=True)
sch.vectorize(loop=l45)
sch.annotate(block_or_loop=l42, ann_key="pragma_auto_unroll_max_step", ann_val=16)
sch.annotate(block_or_loop=l42, ann_key="pragma_unroll_explicit", ann_val=1)
b46 = sch.get_block(name="C", func_name="main")
l47, l48, l49, l50, l51, l52, l53 = sch.get_loops(block=b46)
b54 = sch.decompose_reduction(block=b46, loop=l48)

通过 Schedule 变换的方式，得到原始计算的多种表示，在这多组表示中选择性能最好的，实现了对 TensorIR 加速的目的 auto_prog_optim_transformation_search

端到端模型执行

上面介绍了 TensorIR 及其变换方法，在模型部署过程中常常会涉及多个算子，如下图所示，涉及到了3个 TensorIR：linear0, linear1 和 relu0。

computation_graph

TVM 通过高层 IR 描述了整个模型的执行过程：

@tvm.script.ir_module
class MyModule:
    @T.prim_func
    def relu0(X: T.Buffer[(1, 128), "float32"],
              Y: T.Buffer[(1, 128), "float32"]):
        ...

    @T.prim_func
    def dense0(X: T.Buffer[(1, 784), "float32"],
               W: T.Buffer[(128, 784), "float32"],
               Z: T.Buffer[(1, 128), "float32"]):
        ...

    @T.prim_func
    def add0(X: T.Buffer[(1, 128), "float32"],
             B: T.Buffer[(128,), "float32"],
             Z: T.Buffer[(1, 128), "float32"]):
        ...


    @T.prim_func
    def dense1(X: T.Buffer[(1, 128), "float32"],
               W: T.Buffer[(10, 128), "float32"],
               Z: T.Buffer[(1, 10), "float32"]):
        ...

    @T.prim_func
    def add1(X: T.Buffer[(1, 10), "float32"],
             B: T.Buffer[(10,), "float32"],
             Z: T.Buffer[(1, 10), "float32"]):
        ...

    @R.function
    def main(x: Tensor((1, 784), "float32"),
             w0: Tensor((128, 784), "float32"),
             b0: Tensor((128,), "float32"),
             w1: Tensor((10, 128), "float32"),
             b1: Tensor((10,), "float32")):
        with R.dataflow():
            lv0 = R.call_tir(dense0, (x, w0), (1, 128), dtype="float32")
            lv1 = R.call_tir(add0, (lv0, b0), (1, 128), dtype="float32")
            lv2 = R.call_tir(relu0, (lv1,), (1, 128), dtype="float32")
            lv3 = R.call_tir(dense1, (lv2, w1), (1, 10), dtype="float32")
            out = R.call_tir(add1, (lv3, b1), (1, 10), dtype="float32")
            R.output(out)
        return out

图优化 FuseOps

TVM 支持算子自动融合，融合后 IRModule 如下（此处举例没有融合relu，实际代码执行会融合）。可以看到 fused_dense_add0 和 fused_dense_add1 仍然是上层 relax/relay 函数，它们调用相应的 TensorIR dense 和 add 函数。

@tvm.script.ir_module
class Module:
    @R.function
    def fused_dense_add1(x: Tensor((1, 128), "float32"), w: Tensor((10, 128), "float32"), b: Tensor((10,), "float32")) -> Tensor(None, "float32", ndim = 2):
        ...

    @T.prim_func
    def relu(rxplaceholder: T.Buffer[(1, T.int64(128)), "float32"], compute: T.Buffer[(1, T.int64(128)), "float32"]) -> None:
        ...

    @T.prim_func
    def dense1(rxplaceholder: T.Buffer[(1, T.int64(128)), "float32"], rxplaceholder_1: T.Buffer[(T.int64(10), T.int64(128)), "float32"], T_matmul_NT: T.Buffer[(1, T.int64(10)), "float32"]) -> None:
        ...

    @T.prim_func
    def add1(rxplaceholder: T.Buffer[(1, T.int64(10)), "float32"], rxplaceholder_1: T.Buffer[T.int64(10), "float32"], T_add: T.Buffer[(1, T.int64(10)), "float32"]) -> None:
        ...

    @T.prim_func
    def dense(rxplaceholder: T.Buffer[(1, 784), "float32"], rxplaceholder_1: T.Buffer[(T.int64(128), T.int64(784)), "float32"], T_matmul_NT: T.Buffer[(1, T.int64(128)), "float32"]) -> None:
        ...

    @T.prim_func
    def add(rxplaceholder: T.Buffer[(1, T.int64(128)), "float32"], rxplaceholder_1: T.Buffer[T.int64(128), "float32"], T_add: T.Buffer[(1, T.int64(128)), "float32"]) -> None:
        ...

    @R.function
    def fused_dense_add0(x1: Tensor((1, 784), "float32"), w1: Tensor((128, 784), "float32"), b1: Tensor((128,), "float32")) -> Tensor(None, "float32", ndim = 2):
        # block 0
        with R.dataflow():
            lv1 = R.call_tir(dense, (x1, w1), (1, 128), dtype="float32")
            gv1 = R.call_tir(add, (lv1, b1), (1, 128), dtype="float32")
            R.output(gv1)
        return gv1

    @R.function
    def main(x2: Tensor((1, 784), "float32")) -> Tensor(None, "float32", ndim = 2):
        # block 0
        with R.dataflow():
            lv11: Tensor((1, 128), "float32") = fused_dense_add0(x2, meta[relay.Constant][0], meta[relay.Constant][1])
            lv2 = R.call_tir(relu, (lv11,), (1, 128), dtype="float32")
            lv4: Tensor((1, 10), "float32") = fused_dense_add1(lv2, meta[relay.Constant][2], meta[relay.Constant][3])
            gv2: Tensor((1, 10), "float32") = lv4
            R.output(gv2)
        return gv2

此时的融合实际上只发生在高层 IR 表示上，从底层 IR 的角度去看实际上是没有融合的。还需要额外的工作（FuseTIR）将它们变成一个单一的 TensorIR 函数；实际的 Lower 过程中会跑执行这个逻辑，relax IR 中负责这快处理的逻辑如下：

MLPModelFinal = relax.transform.FuseTIR()(MLPModelTIR)

Lower后的 IRModule 如下，可以看出 TensorIR 层面已经完成了融合：

@tvm.script.ir_module
class Module:
    @T.prim_func
    def fused_dense_add0(x: T.Buffer[(1, 784), "float32"], w: T.Buffer[(T.int64(128), T.int64(784)), "float32"], b: T.Buffer[T.int64(128), "float32"], T_add: T.Buffer[(1, T.int64(128)), "float32"]) -> None:
        # function attr dict
        T.func_attr({"tir.noalias": True, "global_symbol": "fused_dense_add0"})
        # body
        # with T.block("root")
        T_matmul_NT = T.alloc_buffer([1, T.int64(128)], dtype="float32")
        for i0, i1, i2 in T.grid(1, T.int64(128), 784):
            with T.block("T_matmul_NT"):
                i = T.axis.spatial(1, i0)
                j = T.axis.spatial(T.int64(128), i1)
                k = T.axis.reduce(784, i2)
                T.reads(x[i, k], w[j, k])
                T.writes(T_matmul_NT[i, j])
                with T.init():
                    T_matmul_NT[i, j] = T.float32(0)
                T_matmul_NT[i, j] = T_matmul_NT[i, j] + x[i, k] * w[j, k]
        for i0, i1 in T.grid(1, T.int64(128)):
            with T.block("T_add"):
                ax0 = T.axis.spatial(1, i0)
                ax1 = T.axis.spatial(T.int64(128), i1)
                T.reads(T_matmul_NT[ax0, ax1], b[ax1])
                T.writes(T_add[ax0, ax1])
                T_add[ax0, ax1] = T_matmul_NT[ax0, ax1] + b[ax1]

    @T.prim_func
    def relu(rxplaceholder: T.Buffer[(1, T.int64(128)), "float32"], compute: T.Buffer[(1, T.int64(128)), "float32"]) -> None:
        # function attr dict
        T.func_attr({"global_symbol": "relu", "tir.noalias": True})
        # body
        # with T.block("root")
        for i0, i1 in T.grid(1, T.int64(128)):
            with T.block("compute"):
                i0_1 = T.axis.spatial(1, i0)
                i1_1 = T.axis.spatial(T.int64(128), i1)
                T.reads(rxplaceholder[i0_1, i1_1])
                T.writes(compute[i0_1, i1_1])
                compute[i0_1, i1_1] = T.max(rxplaceholder[i0_1, i1_1], T.float32(0))

    @T.prim_func
    def fused_dense_add1(x: T.Buffer[(1, T.int64(128)), "float32"], w: T.Buffer[(T.int64(10), T.int64(128)), "float32"], b: T.Buffer[T.int64(10), "float32"], T_add: T.Buffer[(1, T.int64(10)), "float32"]) -> None:
        # function attr dict
        T.func_attr({"tir.noalias": True, "global_symbol": "fused_dense_add1"})
        # body
        # with T.block("root")
        T_matmul_NT = T.alloc_buffer([1, T.int64(10)], dtype="float32")
        for i0, i1, i2 in T.grid(1, T.int64(10), T.int64(128)):
            with T.block("T_matmul_NT"):
                i = T.axis.spatial(1, i0)
                j = T.axis.spatial(T.int64(10), i1)
                k = T.axis.reduce(T.int64(128), i2)
                T.reads(x[i, k], w[j, k])
                T.writes(T_matmul_NT[i, j])
                with T.init():
                    T_matmul_NT[i, j] = T.float32(0)
                T_matmul_NT[i, j] = T_matmul_NT[i, j] + x[i, k] * w[j, k]
        for i0, i1 in T.grid(1, T.int64(10)):
            with T.block("T_add"):
                ax0 = T.axis.spatial(1, i0)
                ax1 = T.axis.spatial(T.int64(10), i1)
                T.reads(T_matmul_NT[ax0, ax1], b[ax1])
                T.writes(T_add[ax0, ax1])
                T_add[ax0, ax1] = T_matmul_NT[ax0, ax1] + b[ax1]

    @R.function
    def main(x: Tensor((1, 784), "float32")) -> Tensor(None, "float32", ndim = 2):
        # block 0
        with R.dataflow():
            lv1 = R.call_tir(fused_dense_add0, (x, meta[relay.Constant][0], meta[relay.Constant][1]), (1, 128), dtype="float32")
            lv2 = R.call_tir(relu, (lv1,), (1, 128), dtype="float32")
            lv4 = R.call_tir(fused_dense_add1, (lv2, meta[relay.Constant][2], meta[relay.Constant][3]), (1, 10), dtype="float32")
            gv: Tensor((1, 10), "float32") = lv4
            R.output(gv)
        return gv

TVM 编译器可以通过自动图优化手段，在计算图之间进行变换，并在后续的 Lower 工作中，将相应的融合反馈到 TensorIR 中。接下来又回到了 TensorIR + Schedule 变换的主题中。

手工优化一般从计算图融合和优化算子性能两个角度考虑，定制化程度高；编译器的优化思路整体而言和手工优化类似，通过自动化的手段对 IRModule 进行变换（图变换和 schedule 变换），通用化程度较高。

调用外部库

目前已经存在较多高度优化的矩阵计算库如 mkl, cublas, cudnn, cutlass 等被各行各业使用，通过编译器自动优化的方式很难在较短时间内搜索到能够与之匹敌的算法，鉴于此原因，希望将现有的库函数集成到 MLC 的过程中。

首先将已有的库函数注册到 TVM 中：

@tvm.register_func("env.linear", override=True)
def torch_linear(x: tvm.nd.NDArray,
                 w: tvm.nd.NDArray,
                 b: tvm.nd.NDArray,
                 out: tvm.nd.NDArray):
    x_torch = torch.from_dlpack(x)
    w_torch = torch.from_dlpack(w)
    b_torch = torch.from_dlpack(b)
    out_torch = torch.from_dlpack(out)
    torch.mm(x_torch, w_torch.T, out=out_torch)
    torch.add(out_torch, b_torch, out=out_torch)

@tvm.register_func("env.relu", override=True)
def lnumpy_relu(x: tvm.nd.NDArray,
                out: tvm.nd.NDArray):
    x_torch = torch.from_dlpack(x)
    out_torch = torch.from_dlpack(out)
    torch.maximum(x_torch, torch.Tensor([0.0]), out=out_torch)

只要修改高层 IR 中对计算的描述，调用外部注册的函数即可：

@tvm.script.ir_module
class MyModuleWithExternCall:
    @R.function
    def main(x: Tensor((1, 784), "float32"),
             w0: Tensor((128, 784), "float32"),
             b0: Tensor((128,), "float32"),
             w1: Tensor((10, 128), "float32"),
             b1: Tensor((10,), "float32")):
        # block 0
        with R.dataflow():
            lv0 = R.call_tir("env.linear", (x, w0, b0), (1, 128), dtype="float32")
            lv1 = R.call_tir("env.relu", (lv0,), (1, 128), dtype="float32")
            out = R.call_tir("env.linear", (lv1, w1, b1), (1, 10), dtype="float32")
            R.output(out)
        return out

总结

机器学习编译的基本思想同手工优化相似，主要是通过计算图融合和优化单个算子的性能两种方式来提升模型的性能；编译器在计算图融合上更进一步，从过去的特定模板匹配的方式进化成按规则匹配，由处理单个算子的匹配规则到处理一类算子；在算子性能优化上，TVM 编译器采用计算调度分离的方式，通过自动程序优化的手段来寻找更优的算子实现，如果搜索到的算子性能都不理想，也可以通过调用外部库来实现。

手工优化也可以尝试和编译器优化结合来提升模型的性能，例如在编译器优化的基础上，通过手工优化的方式来调整算子的实现；在有先验知识的情况下，可以通过先走指定的图融合策略，后面再去运行编译器自动融合的 pass 来修正图融合的结果等。

References

https://mlc.ai/
https://tvm.apache.org/docs/arch/index.html
https://zhuanlan.zhihu.com/p/589619468