Linear Model

设$x_1$和$x_2$是两个标量或维数相同的向量，$\alpha$和$\beta$为任意标量，则称$\alpha x_1 + \beta x_2$为$x_1$和$x_2$的线性组合。若$f$为$x$的线性函数，则有\[f(\alpha x_1 + \beta x_2) = \alpha f(x_1) + \beta f(x_2)\] 简言之，一些输入参数的线性组合的函数值等于其函数值的线性组合。

Linear Regression

所谓回归即依据样本集$x_i, f(x_i)$来学习一个函数估计子$\hat{f} : \chi \rightarrow \mathbb{R}$

我们将$y$近似为$x$的线性函数\[h_{\theta}(x)=\theta_0+\theta_1 x_1 + \theta_2 x_2 + \cdots\]也可以写成\[h(x) = \sum_{i=0}^{n} \theta_i x_i = \theta^T x \]

定义代价函数\[J(\theta) = \frac {1}{2} \sum_{i=1}^{m} (h_\theta (x^{(i)})-y^{(i)})^2\]

对该代价函数的优化有多种方法：最小二乘法（一元线性回归）、正规方程（多元线性回归）和梯度下降法，其中最小二乘法和正规方程可得到封闭解。下面依次介绍上述方法。

OLS

最小二乘法适用于一元线性回归的情况，假设存在线性关系$y=a+bx$其中$a$和$b$是两个能够使得残差的平方和$\sum_{i=1}^{n}(y_i-(a+b x_i))^2$为最小的两个参数，为求取这两个参数，可对表达式分别对$a$和$b$求偏导，并令其为0。

[\frac {\partial}{\partial a} \sum_{i=1}^{n} (y_i - (a+b x_i))^2 = -2\sum_{i=1}^{n} (y_i - (a+b x_i)) = 0]

[\frac {\partial}{\partial b} \sum_{i=1}^{n} (y_i - (a+b x_i))^2 = -2\sum_{i=1}^{n} (y_i - (a+b x_i))x_i = 0]

可以解得

[\hat{a} \Rightarrow \overline{y} - \hat{b} \overline{x}]

[\hat{b} \Rightarrow \frac {\sum_{i=1}^{n} x_i y_i - n \overline{x} \overline{y}}{\sum_{i=1}^{n} x_i^2 - n \overline{x}^2} = \frac {\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})}{\sum_{i=1}^{n}(x_i-\overline{x})^2}]

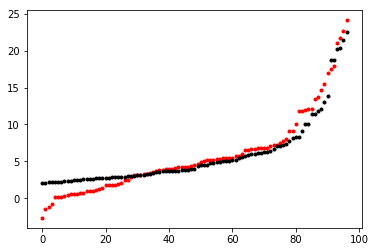
接下来使用最小二乘法拟合一组数据，数据可从link处下载。最小二乘法代码见link

原数据与线性模型可视化如下图所示 ols

Norm Equation

正规方程能够求取多元线性回归的封闭解，给定训练集$m\times n$矩阵X（包含截距项则为$m \times n+1$），其中矩阵每一行都为训练集的一个实例。

[X=\begin{bmatrix} -(x^{(1)})^T-
-(x^{(2)})^T-
\vdots
-(x^{(m)})^T-
\end{bmatrix}]

$\vec{y}$为$m$维向量，包含对应训练集特征的所有目标值。

[\vec{y}=\begin{bmatrix} y^{(1)}
y^{(2)}
\vdots
y^{(m)}
\end{bmatrix}]

又因为$h_{\theta}(x^{(i)})=(x^{(i)})^T \theta$可得

[\begin{equation}\begin{split} X \theta-\vec{y} &= \begin{bmatrix} (x^{(1)})^T
\vdots
(x^{(m)})^T
\end{bmatrix} - \begin{bmatrix} y^{(1)}
\vdots
y^{(m)}
\end{bmatrix}
&=\begin{bmatrix} h_{\theta}(x^{(i)}) - y^{(1)}
\vdots
h_{\theta}(x^{(m)}) - y^{(m)}
\end{bmatrix}

\end{split}\end{equation}]

考虑到$\vec{z}^T\vec{z}=\sum_iz_i^2$可知

[\begin{equation}\begin{split} \frac {1}{2} (X\theta-\vec{y})^T(X\theta-\vec{y})&=\frac {1}{2}\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2
&=J(\theta) \end{split}\end{equation}]

为了最小化$J(\theta)$需要对每一个$\theta$求导，即$\nabla_{\theta}J(\theta)$，在此先介绍矩阵迹的性质

$\nabla_AtrAB = B^T$ $\nabla_{A^T}f(A)=(\nabla_Af(A))^T$ $\nabla_AtrABA^TC=CAB+C^TAB^T$

有了上述公式，即可求解$\nabla_{\theta}J(\theta)$

[\begin{equation}\begin{split} \nabla_{\theta}J(\theta) &= \frac {1}{2} (X\theta-\vec{y})^T(X\theta-\vec{y})
&=\frac {1}{2} \nabla_{\theta}(\theta^TX^TX\theta - \theta^TX^T\vec{y}-\vec{y}^TX\theta+\vec{y}^T\vec{y})
&=\frac {1}{2} \nabla_{\theta}tr(\theta^TX^TX\theta - \theta^TX^T\vec{y}-\vec{y}^TX\theta+\vec{y}^T\vec{y})
&=\frac {1}{2} \nabla_{\theta}(tr\theta^TX^TX\theta -2tr\vec{y}^TX\theta)
&=\frac {1}{2}(X^TX\theta + X^TX\theta - 2X^T\vec{y})
&=X^TX\theta - X^T\vec{y} \end{split}\end{equation}]

该证明第三步我们利用了标量的迹为其本身；第四步利用了$trA=trA^T$；第五步令$A^T=\theta, B=B^T=X^TX, C=I$，则利用该公式$\nabla_{A^T}trABA^TC=B^TA^TC^T+BA^TC=$可化简。为使得$J$最小，令导入为0，得到正规方程

[X^TX\theta = X^T\vec{y}]

因此，可以得到$\theta$的封闭解

[\theta=(X^TX)^{-1}X^T\vec{y}]

接下来利用正规方程求解多元线性回归问题，数据可从link处下载，代码见link

Gradient Descent

梯度下降在机器学习和深度学习中有相当重要的作用，所以本人准备另写一篇关于梯度下降的博客详细的介绍原理以及实现link。这里不在叙述。

这里利用tensorflow和numpy解决上述的预测房价问题。

Tensorflow

这里利用tensorflow框架来优化多元线性回归问题，代码中包括了简单的数据预处理，使得Loss近似为0。数据可从link处下载，代码见link

Python + Numpy

这里利用python和numpy在多元线性回归条件下实现简单的梯度下降，代码中包括了简单的数据预处理，最终loss近似为0。数据可从link处下载，代码见link

引用

http://ufldl.stanford.edu/tutorial/supervised/LinearRegression/
http://cs229.stanford.edu/notes/cs229-notes1.pdf
Peter Flach.机器学习[M].北京:人民邮电出版社.2016.