GAN

1. 初识GAN

GAN模型中包含两个网络：生成器G和判别器D。G用来捕捉训练集数据的分布，D用来判别数据来自训练集还是生成器。

对该模型的优化需要同时训练G和D：训练D的目的是最大化判别器D的判别准确率，训练G的目的是最小化判别器D的判别准确率。这种问题理论上存在唯一最优解：生成器可以还原数据分布\(p_g=p_{data}\)，判别器D=\(\frac 12\)。

定义先验噪声变量\(p_z(z)\)，噪声映射数据空间函数\(G(z;\theta_g)\)，G是由包括参数\(\theta_g\)的多层神经网络。我们又定义了多层神经网络\(D(x;\theta_d)\)输出单一的标量。\(D(x)\)代表了数据来自训练集而不是生成器的概率。训练判别器D来最大化分配正确标签给训练集和生成器的概率，公式见（1.1）。训练生成器G最小化\(log(1-D(G(z)))\)。综上所述，定义目标函数见公式（1.2）。 \[\operatorname*{max}_D\left.V(D,G)\right. = E _{x \sim p _{data}}[log(D(X))] + E _{z \sim p _z(z)}[log(1-D(G(z)))]\tag{1.1}\]

\[\operatorname*{minmax}_{G \quad D}\left.V(D,G)\right. = E _{x \sim p _{data}}[log(D(X))] + E _{z \sim p _z(z)}[log(1-D(G(z)))]\tag{1.2}\]

如果我们把生成模型比作是一个伪装者的话，那么判别模型就是一个警察的角色。伪装者的目的，就是通过不断的学习来提高自己的伪装能力，从而使得自己提供的数据能够更好地欺骗这个判别模型。而判别模型则是通过不断的训练来提高自己判别的能力，能够更准确地判断数据来源究竟是哪里。 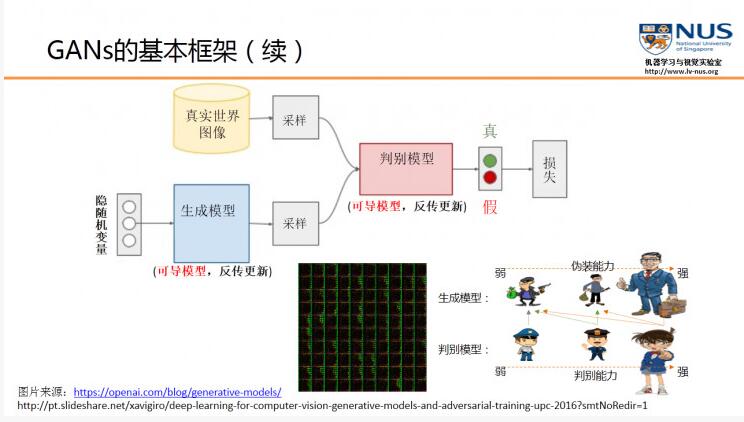Weibo 当一个判别模型的能力已经非常强的时候，如果生成模型所生成的数据，还是能够使它产生混淆，无法正确判断的话，那我们就认为这个生成模型实际上已经学到了真实数据的分布。
接下来，通过实现两个简单的例子，来更深入的体会GAN的核心思想。

2. GAN生成一维数据

接下来，我们使用pytorch框架，通过一个简单的例子来了解GAN。首先给定一个均值为4，方差为1.25的正态分布作为我们要生成的一维数据，使用0到1的平均分布作为噪声输入，搭建GAN模型，使得生成器的输出与上文提到的\(N(4，1.25)\) 正态分布类似。（完整代码见code）

定义判别器

class Discriminator(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Discriminator, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.fc2 = nn.Linear(hidden_size, hidden_size)
        self.fc3 = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        x = F.elu(self.fc1(x))
        x = F.elu(self.fc2(x))
        return F.sigmoid((self.fc3(x)))

定义生成器

class Generator(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Generator, self).__init__()
        self.dim = dim
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.fc2 = nn.Linear(hidden_size, hidden_size)
        self.fc3 = nn.Linear(hidden_size, output_size)

    def forward(self, x):        
        x = F.elu(self.fc1(x))
        x = F.sigmoid(self.fc2(x))
        return self.fc3(x)

搭建模型

G = Generator(input_size=g_input_size, hidden_size=g_hidden_size, output_size=g_output_size)
D = Discriminator(input_size=d_input_func(d_input_size), hidden_size=d_hidden_size, output_size=d_output_size)
criterion = nn.BCELoss()
d_optimizer = optim.Adam(D.parameters(), lr=d_learning_rate, betas=optim_betas)
g_optimizer = optim.Adam(G.parameters(), lr=g_learning_rate, betas=optim_betas)

模型训练

for epoch in range(num_epochs):
    for d_index in range(d_steps):
        # 1. Train D on real+fake
        D.zero_grad()
        #  1A: Train D on real
        d_real_data = Variable(d_sampler(d_input_size))
        d_real_decision = D(preprocess(d_real_data))
        d_real_error = criterion(d_real_decision, Variable(torch.ones(1) * 0.95))
        d_real_error.backward()  

        #  1B: Train D on fake
        d_gen_input = Variable(gi_sampler(minibatch_size, g_input_size))
        d_fake_data = G(d_gen_input).detach()  # detach to avoid training G on these labels
        d_fake_decision = D(preprocess(d_fake_data.t()))
        d_fake_error = criterion(d_fake_decision, Variable(torch.zeros(1) * 0.95))
        d_fake_error.backward()
        d_optimizer.step()

    for g_index in range(g_steps):
        # 2. Train G on D's response (but DO NOT train D on these labels)
        G.zero_grad()

        gen_input = Variable(gi_sampler(minibatch_size, g_input_size))
        g_fake_data = G(gen_input)
        dg_fake_decision = D(preprocess(g_fake_data.t()))
        g_error = criterion(dg_fake_decision, Variable(torch.ones(1) * 0.95))  

        g_error.backward()
        g_optimizer.step()  

    if epoch % print_interval == 0:
        print("%s: D: %s/%s G: %s (Real: %s, Fake: %s) " % (epoch,
                                                            extract(d_real_error)[0],
                                                            extract(d_fake_error)[0],
                                                            extract(g_error)[0],
                                                            stats(extract(d_real_data)),
                                                            stats(extract(d_fake_data))))
        torch.save(D.state_dict(), 'd.pkl')
        torch.save(G.state_dict(), 'g.pkl')

查看生成的数据

模型训练完毕后，加载训练好的模型，随机产生一些均匀分布的数据，观察生成数据的直方图。

if os.path.exists('g.pkl'):
    G.load_state_dict(torch.load('g.pkl'))
if os.path.exists('d.pkl'):
    D.load_state_dict(torch.load('d.pkl'))
fake_data = G(Variable(gi_sampler(1000, 1)))
fake_data = fake_data.data.numpy()
print(np.mean(fake_data), np.std(fake_data))
plt.hist(fake_data, bins=100)
plt.show()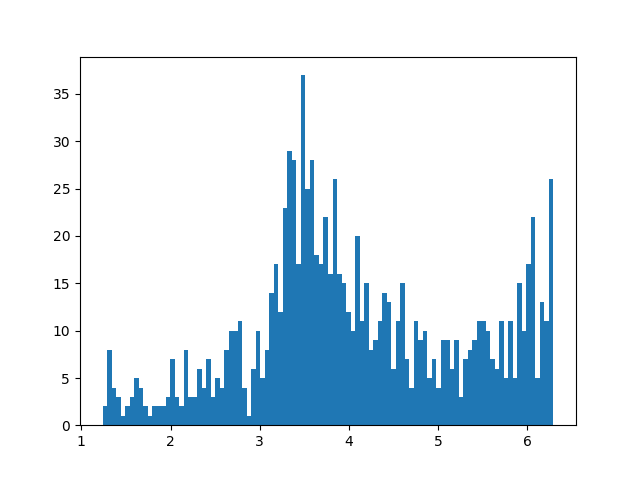

生成数据直方图发现生成的数据均值为3.5，方差1.15左右，我们可以肯定生成器已经学到了训练数据部分信息，但是该结果并不太令人满意，因为我们期望均值为4，方差为1.25，而且经过多次调参后，发现一个问题：得到的均值和方差满足要求，但是生成数据的分布完全走形，GAN太过敏感，超参数的选择比较困难。

3. MNIST

与使用GAN生成一维数据原理相同，我们使用GAN来生成MNIST数据。完整代码见code

生成器

对上面的生成器添加dropout层，并且添加激活层tanh。

class Generator(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Generator, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.fc2 = nn.Linear(hidden_size, hidden_size)
        self.fc3 = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        x = F.dropout(F.relu(self.fc1(x)), p=0.2)
        x = F.dropout(F.relu(self.fc2(x)), p=0.2)
        return F.tanh(self.fc3(x))

判别器

对上述判别器添加dropout层，其余相同

class Discriminator(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1):
        super(Discriminator, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.fc2 = nn.Linear(hidden_size, hidden_size)
        self.fc3 = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        x = F.dropout(F.relu(self.fc1(x)), p=0.2)
        x = F.dropout(F.relu(self.fc2(x)), p=0.2)
        return F.sigmoid((self.fc3(x)))

搭建模型

与上述类似，在此我们将整个模型封装成一个类，供外部调用

def build_model(self):
    self.G = Generator(input_size=self.g_input_size, hidden_size=self.g_hidden_size,
                       output_size=self.g_output_size)
    self.D = Discriminator(input_size=self.d_input_size, hidden_size=self.d_hidden_size,
                           output_size=self.d_output_size)
    self.load_model()
    self.criterion = nn.BCELoss()
    self.d_optimizer = optim.Adam(self.D.parameters(), self.d_lr, betas=self.betas)
    self.g_optimizer = optim.Adam(self.G.parameters(), self.g_lr, betas=self.betas)

模型训练

由于没有GPU，只能使用CPU进行训练，这一步需要等很长很长很长时间。。。。

def fit(self, real_x):
    for epoch in range(self.num_epoch):
        for i, real_x_batch in enumerate(self.gen_batch(real_x)):
            d_real_data = Variable(torch.from_numpy(real_x_batch.astype(np.float32)))
            gen_norm_data = np.random.uniform(-1, 1, size=(self.batch_size, 100))
            d_fake_input = Variable(torch.from_numpy(gen_norm_data.astype(np.float32)))
            d_real_error_sum = 0.0
            d_fake_error_sum = 0.0
            g_error_sum = 0.0

            # Train D
            for _ in range(self.d_steps):
                self.D.zero_grad()
                d_real_decision = self.D(d_real_data)
                d_real_error = self.criterion(d_real_decision,
                                              Variable(torch.ones(self.batch_size, 1)) * (1 - self.smooth))
                d_fake_data = self.G(d_fake_input).detach()
                d_fake_decision = self.D(d_fake_data)
                d_fake_error = self.criterion(d_fake_decision,
                                              Variable(torch.zeros(self.batch_size, 0) * (1 - self.smooth)))
                d_error = d_fake_error + d_real_error
                d_error.backward()
                self.d_optimizer.step()

                d_real_error_sum += d_real_error.data[0]
                d_fake_error_sum += d_fake_error.data[0]

            # Train G
            for _ in range(self.g_steps):
                self.G.zero_grad()

                gen_input = d_fake_input
                g_fake_data = self.G(gen_input)
                dg_fake_decision = self.D(g_fake_data)
                g_error = self.criterion(dg_fake_decision,
                                         Variable(torch.ones(self.batch_size, 1) * (1 - self.smooth)))
                g_error.backward()
                self.g_optimizer.step()

                g_error_sum += g_error.data[0]

            if (i + 1) % self.print_interval == 0:
                print("%s/%s--%s/%s: D: %s/%s G: %s)" % (
                    epoch, self.num_epoch,
                    i, len(real_x) // self.batch_size,
                    d_real_error_sum / self.print_interval,
                    d_fake_error_sum / self.print_interval,
                    g_error_sum / self.print_interval
                ))
                d_real_error_sum = 0.0
                d_fake_error_sum = 0.0
                g_error_sum = 0.0

        d_fake_data = self.G(Variable(
            torch.from_numpy(np.random.uniform(-1, 1, size=(self.sample_size, 100)).astype(np.float32))))
        self.save_sample_img(d_fake_data.data.numpy(), epoch)

        if (epoch + 1) % 10 == 0:
            self.save_model(epoch)

生成图片

模型训练过程中最后一个epoch生成的图片，可以看到生成的图片大致与mnist数据集相似，但还是不够清晰，可以适当的减小学习效率和增大迭代次数来生成比较真实的图像

fake_mnist_train

使用训练好的模型生成图片

def show_sample_img(data):
    fig, axes = plt.subplots(figsize=(7, 7), nrows=5,
                             ncols=5,
                             sharex=True, sharey=True)
    for ax, img in zip(axes.flatten(), data):
        ax.xaxis.set_visible(False)
        ax.yaxis.set_visible(False)
        im = ax.imshow(img.reshape((28, 28)), cmap='Greys_r')
    # plt.savefig('fake_samples.png')
    plt.show()
    return fig, axes

fake = np.random.uniform(-1, 1, size=(25, 100))
res = model.sampler(fake)
show_sample_img(res)

fake_mnist_sample

总结

通过这两个实例，可以对GAN的基本思想有初步的把握，但是在训练的过程中发现，GAN训练过程中极不稳定，超参数的选择比较困难，而且计算量较大，没有GPU的机器十分吃力。该模型的优点就是不需要懂太多知识，就可以使用模型生成各种数据。等手上有N卡的电脑后，我会继续更新，将本文训练的模型在优化下，将那些不怎么好看的图片都给替换掉，也会继续使用Pytorch实现GAN变体如条件GAN、DCGAN、InfoGAN以及著名的Wasserstein GAN等。

1. 初识GAN

2. GAN生成一维数据

定义判别器

定义生成器

搭建模型

模型训练

查看生成的数据

3. MNIST

生成器

判别器

搭建模型

模型训练

生成图片

总结

代码链接

引用致谢